Abbott的复仇

题目链接

UVA-816

/*
样例输入：
3 1 N 3 3 
1 1 WL NR * 
1 2 WLF NR ER * 
1 3 NL ER * 
2 1 SL WR NF * 
2 2 SL WF ELF * 
2 3 SFR EL * 
0
样例输出：
(3,1) (2,1) (1,1) (1,2) (2,2) (2,3) (1,3) (1,2) (1,1) (2,1) (2,2) (1,2) (1,3) (2,3) (3,3)
*/

题目分析

在做一道算法题目的时候，我认为真正地搞懂题目意思是非常重要的，题目搞不懂很可能会出现漏解的情况。我觉得从样例输入和输出出发，然后往题目中带，是比较好的理解方式。这道题目结合下图的理解如下：这个图我根据样例走了一遍，为防止混乱，先使用红色，当节点重复了再用蓝色，然后再用绿色，最终走到终点。

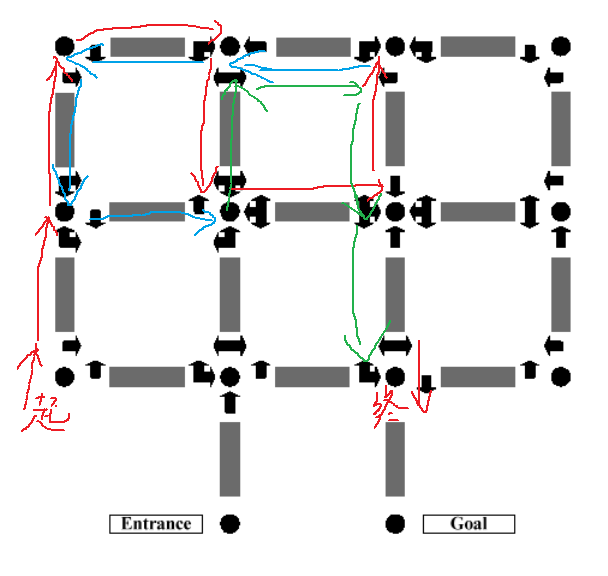
​ 首先看样例输入的第一行，一个起点坐标(3,1)代表第三行第一列，一个离开起点时的位置N代表离开起点时朝向上，一个终点坐标(3,3)代表第三行第三列。一开始的时候我是有点疑问的：为什么上图的最下面有两个点表示起点和终点和样例中的不太一样啊，可后来想了想，样例输出可以有很多的，题目中的图只代表了一种情况，所以不用管多余的点。

​ 然后看每一个坐标，都有进入坐标的方向，即NEWS，分表表示上、右、左、下，LFR分别表示进入该点可以向左、直走、向右走。结合样例比如1 1 WL NR*，对应图中的(1,1)坐标点，表示当进入(1,1)时的方向，如果是W，即向左的话，那么此时你只能左转；如果进入(1,1)朝向向上的话，此时只能右转，输入*代表此节点的输入结束，接着读取下一行，然后输入0代表整个输入结束。

研究对象

​ 说是研究对象可能有点过了，这里我指的是在算法解决问题的过程中所定义的几个重要的变量，下面针对我认为很重要的变量解释一波。

/*
1、Node结构体：这是一个三元组，用来表示位于(r,c)位置，dir表示方向朝向
2、has_edge[r][c][dir][turn]数组：这个四维数组表示当前状态是(r,c,dir)，是否可以朝turn转向。初始化为0，设为1表示可以转向。
3、d[r][c][dir]数组：该数组表示记录当前状态的节点与初始化状态的节点的距离。该数组初始化为-1。并且起点为-1，与题目意思切合，起点的下一个位置才是初始状态，所以下一个位置为0，所以也可以认为d数组是用来记录移动次数的，每移动一个节点值加一。方便打印的时候从跟节点回溯。
4、p[r][c][dir]数组：该数组表示了(r,c,dir)在BFS树中的父节点，在BFS树中除了起点外，每个节点都有唯一一个父节点。
*/

研究方法

对用来解决问题的函数方法先说明一下。

• read_case();该方法是将所有的输入转换到has_edge数组中，表示此状态下节点所允许的转向。结合上图的BFS树理解也就是在该节点状态下有几个分支可以走。

• dir_id();将NESW四个方向转换为0~3整数，方便在数组中当下标使用。

• turn_id();将FLR三个转向转换为0~2整数，方便在数组中当下标使用。

• walk();这个函数极为巧妙，用来获取转向后的下一个状态。根据FLR三种不同的转向，如果转向为L，即向左转，那么就顺时针加三，比如此时朝向为S，转向为L，那么在现实中我们很容易想到就是E，但是利用代码的话就是(dir+3)%4，这里为什么要用加？这是因为用加的话取余就可以再次从头开始循环NESW，但是逻辑上应该是逆时针减一的;如果转向为R，即向右转，那么就顺时针加一；如果转向为F，那么dir方向不变。

  可以画一下图，一下子就理解了，见下图。

  

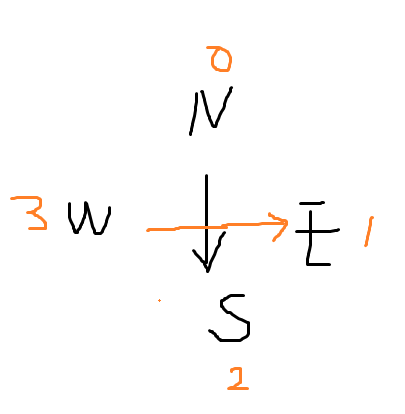
• solve();利用BFS方法模拟走路，分别查看FLR三个转向能否走，也就是层次遍历的核心了。然后每走一步就在上面定义的数组中更新一下状态，并把当前满足条件的分支加入到队列中。思路见下图。

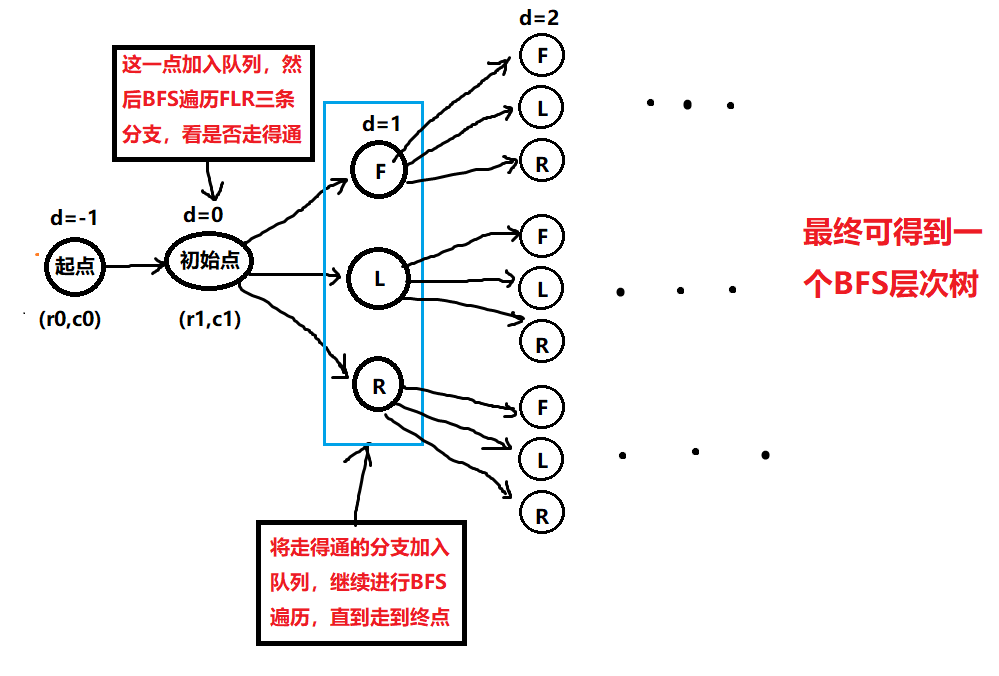
最终可得到类似下图的BFS层次树

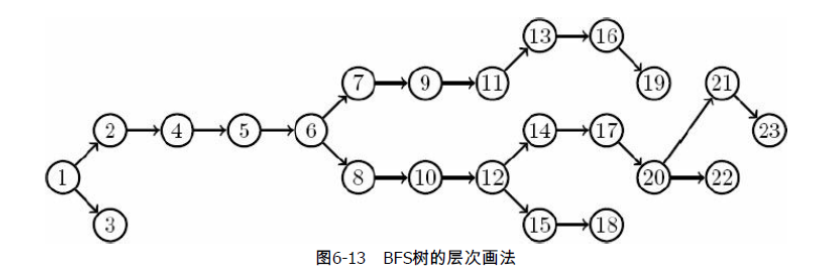
代码实现

​ 下面就将详细的解题思路注释在代码中，有时候看代码比看文字理解起来更容易。

#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;

struct Node{
	int r,c,dir;//站在(r,c)点，面朝方向dir(0~3)分别表示N,E,S,W
	Node(int r=0,int c=0,int dir=0):r(r),c(c),dir(dir){}
};

const char* dirs="NESW";//上0 右1 下2 左3 
const char* turns="FLR";//直行0 左转1 右转2
const int maxn=10;
const int dr[]={-1,0,1,0};//这两个数组用来根据朝向设置移动步数，0~3下标分别对应NESW 
const int dc[]={0,1,0,-1};
int has_edge[maxn][maxn][4][3];//节点可能的转向 
int d[maxn][maxn][4];//记录此时与起点的距离 
Node p[maxn][maxn][4];//记录此节点的直接父节点
 
//定义起点坐标、离开起点时方向、初始状态坐标和终点坐标 
int r0,c0,dir,r1,c1,r2,c2;

//将字符NESW，方位的顺时针转为从0~3的整数 
int dir_id(char c) {
	return strchr(dirs,c)-dirs;
} 
//将转向数组转为0~2的整数
int turn_id(char c){
	return strchr(turns,c)-turns;
}
//输入函数，初始化起点终点和每一个坐标的专线 
bool read_case(){
	//ch用来读取离开初始位置的方向,s用来读取每个节点可能的转向 
	char ch[maxn],s[maxn];
	if(scanf("%d%d%s%d%d",&r0,&c0,&ch,&r2,&c2)!=5) return false;
	dir=dir_id(ch[0]);
	r1=r0+dr[dir];//这个是离开起点的第一个位置，即初始状态 
	c1=c0+dc[dir];
	int r,c;
	memset(has_edge,0,sizeof(has_edge));	
	while(true){
		scanf("%d",&r);
		if(r==0) break;
		scanf("%d",&c);
		while(scanf("%s",s)==1&&s[0]!='*'){
			int d=dir_id(s[0]);
			for(int i=1;i<strlen(s);i++){
				int t=turn_id(s[i]);
				has_edge[r][c][d][t]=1; 
			}
		}
	} 
	return true;
}
//根据转向更新节点 
Node walk(Node u,int turn){
	int dir=u.dir;
	if(turn==1) dir=(dir+3)%4;//如果转向为L，更新转向为顺时针数三个位置 
	if(turn==2) dir=(dir+1)%4;//如果转向为R，更新转向为顺时针数一个位置 
	return Node(u.r+dr[dir],u.c+dc[dir],dir); 
}	
//判断数组是否出界
bool inside(int r,int c){
	return r>=1&&r<=9&&c>=1&&c<=9;
} 
//打印路径
void print_ans(Node u){
	//从终点向起点添加到vector中，然后反向遍历输出路径 
	vector<Node> nodes;
	while(true){
		nodes.push_back(u); 
		if(d[u.r][u.c][u.dir]==0) break;//此时跳出循环，为初始状态节点，但不是起点 
		u=p[u.r][u.c][u.dir];//把这个节点的父节点找出来，再加入到向量中 
	}
	nodes.push_back(Node(r0,c0,dir));//记得把起点加入到vector中
	//最后反向遍历，每十个为一行输出路径
	int end=nodes.size()-1;
	int cnt=0;
	for(int i=end;i>0;i--){
		printf("(%d,%d) ",nodes[i].r,nodes[i].c);
		if(++cnt%10==0) printf("\n");
	} 
	printf("(%d,%d)\n",nodes[0].r,nodes[0].c);
} 

//BFS层次数模拟走路 
void solve(){
	queue<Node> q;
	memset(d,-1,sizeof(d));
	Node u(r1,c1,dir);//走了一步之后的初始状态
	d[u.r][u.c][u.dir]=0;//每走一步加一 
	q.push(u);//在这里先把初始状态放入队列，然后在while中操作 
	while(!q.empty()){
		Node u=q.front();q.pop();
		if(u.r==r2&&u.c==c2){//如果走到终点 
			print_ans(u);//打印路径 
			return;//跳出solve函数 
		}
		//不是终点的话就继续走我认为从这个for循环开始体现BFS的核心思想了 
		//循环三次0~2，表示能否转向FLR,在BFS层次树上体现的是遍历三个分支
		for(int i=0;i<3;i++){
			Node v=walk(u,i);
			if(has_edge[u.r][u.c][u.dir][i]&&//这里要看当前节点是否可以分支转向！！！ 
				inside(v.r,v.c)&&
				d[v.r][v.c][v.dir]<0){//这里小于0的意思是之前走过的路不能再走了，再走就闭合了 
				d[v.r][v.c][v.dir]=d[u.r][u.c][u.dir]+1;//更新层次，在上一层的基础上加一，即到起点的距离加一 
				p[v.r][v.c][v.dir]=u;//把u作为v的直接父节点，v是u的下一步之后的要想清楚 
				q.push(v);//把下一步的节点放入队列，方便下一轮的BFS遍历 
			}
		} 	
	}	
	//当没有走到终点的情况下队列为空了，就说明可能无解！ 
	printf("No solution possible\n"); 
}
int main(){
	while(read_case()){
		solve();
	}	
	return 0;
}

运行结果如下：

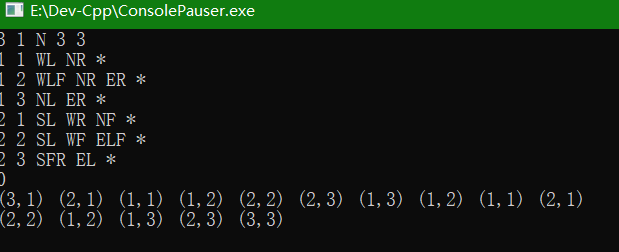
第二次代码实现

#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;
struct Node{
	int r,c,dir;
	Node(int r=0,int c=0,int dir=0):r(r),c(c),dir(dir){}//赋初值，不然声明会报错 
};
const int maxn=10;
const char* dirs="NESW";//定义方向
const char* turns="FLR";//定义转向 
const int dr[]={-1,0,1,0};//定义纵向步长 
const int dc[]={0,1,0,-1};//定义横向步长
int has_edge[maxn][maxn][4][3];//定义方向状态数组 
int d[maxn][maxn][4];//定义此节点在层次树中的层数，也可以说是节点距离起点的距离
Node p[maxn][maxn][4];//记录此节点的上一个节点即直接父节点 
//起点、离开起点时的方向、初始状态、终点
int r0,c0,dir,r1,c1,r2,c2; 

//方向转ID 
int dirs_id(char ch){
	return strchr(dirs,ch)-dirs;
}
//转向转ID
int turns_id(char ch){
	return strchr(turns,ch)-turns;
} 
//读取输入 
bool read_case(){
	char ch[maxn],s[maxn];
	if(scanf("%d%d%s%d%d",&r0,&c0,ch,&r2,&c2)!=5) return false;
	dir=dirs_id(ch[0]);
	
	r1=r0+dr[dir];//设置初始状态点 
	c1=c0+dc[dir];
	//依次读取每个节点的方向状态，用数组保存
	int r,c;
	//每次读入前先将方向状态数组初始化
	memset(has_edge,0,sizeof(has_edge)); 
	while(true){
		scanf("%d",&r);
		if(r==0) break;
		scanf("%d",&c);
		
		while(scanf("%s",s)==1&&s[0]!='*'){
			int d=dirs_id(s[0]);
			int len=strlen(s);
			for(int i=1;i<len;i++){
				has_edge[r][c][d][turns_id(s[i])]=1;
			}
		}
		
	} 
	
	return true;
}
//打印输出最短路径 
void print_ans(Node u){
	vector<Node> nodes;
	while(true){
		nodes.push_back(u);
		if(d[u.r][u.c][u.dir]==0) break;
 		u=p[u.r][u.c][u.dir];		
	}
	//然后把起点加上
	nodes.push_back(Node(r0,c0,dir));
	//倒序输出
	int end=nodes.size()-1;
	int cnt=0;
	for(int i=end;i>0;i--){
		printf("(%d,%d) ",nodes[i].r,nodes[i].c);
		if(++cnt%10==0) printf("\n");
	} 
	printf("(%d,%d)\n",nodes[0].r,nodes[0].c);	
}
//根据转向移动一步 
Node walk(Node u,int turn){
	int dir=u.dir;
	if(turn==1) dir=(dir+3)%4;
	if(turn==2) dir=(dir+1)%4;
	return Node(u.r+dr[dir],u.c+dc[dir],dir);
} 
//判断是否出界 
bool inside(int r,int c){
	return r>=0&&r<=9&&c>=0&&c<=9;
}
//构造bfs层次树 
void bfs(){
	queue<Node> q;
	memset(d,-1,sizeof(d));
	Node u(r1,c1,dir);
	d[u.r][u.c][u.dir]=0;
	q.push(u);
	while(!q.empty()){
		Node u=q.front(); q.pop();
		if(u.r==r2&&u.c==c2){//第一次到达终点直接打印输出 
			print_ans(u);
			return;
		}
		for(int i=0;i<3;i++){//分别看三个转向能否走通 
			Node v=walk(u,i);
			if(has_edge[u.r][u.c][u.dir][i]&&//看此节点状态是否允许转向
				inside(v.r,v.c)&&//看是否出界
				d[v.r][v.c][v.dir]<0//判断是否走过此节点，走过就成环路了 
				){//原来如此，妈的这里竟然忘记括号了 
					d[v.r][v.c][v.dir]=d[u.r][u.c][u.dir]+1;//在层次树中的层次再上一个节点的基础上加一
					p[v.r][v.c][v.dir]=u; //这里一定要记住是把当前节点作为下一个节点的父节点啊 
					q.push(v);//如果走了一步，就加入到队列中 
				}
		}
	}
	//如果走完了还没有到终点，可能无解
	printf("No solution!\n"); 
}

int main(){
	
	while(read_case()){
		bfs();
	}			
	return 0;
}